(Ciencias de Joseleg)(Biología) (Ecología) (La
comunidad) (Introducción) (Generalidades)
(Competencia
interespecífica) (Relación
depredador-presa) (Tácticas
de los depredadores) (Tácticas
de las presas) (La
simbiosis) (Carroñeo)
(Modelo
matemático) (Estructura)
(Interacciones
indirectas) (Gremios
y especies clave) (Biodiversidad)
(Medición
de la biodiversidad) (Sucesiones
ecológicas) (Referencias
bibliográficas)
La mayoría de las personas normalmente no asocian a las matemáticas con la ecología. Sin embargo, la matemática de la ecología se ha convertido en la parte teórica que sustenta casi todos los modelos que nos permiten entender el funcionamiento de los ecosistemas, y también puede decirse que fueron el fundamento base sobre el cual Charles Darwin propuso su entonces hipótesis de selección natural para explicar la evolución y diversidad de los seres vivos. Los ecólogos están interesados en como las poblaciones, comunidades y ecosistemas cambian en el tiempo y en el espacio. En la actualidad las matemáticas que estudian esto se denomina de forma concreta como la Teoría de Sistemas Dinámicos que junto con la Teoría de Redes son la base teórica de la ecología moderna.
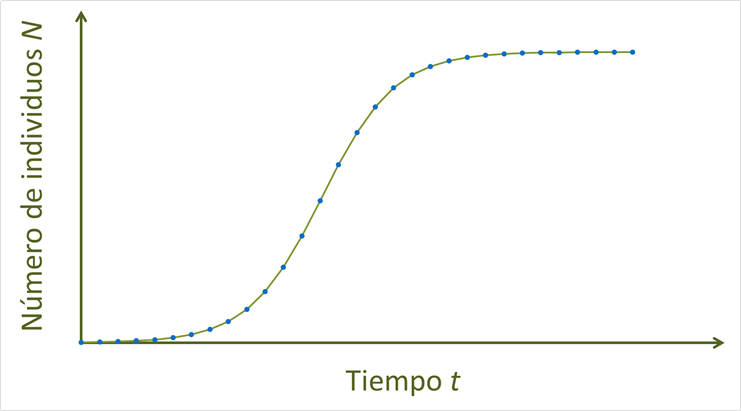
Figura 54. Modelo logístico. El modelo
exponencial es una aproximación al promedio de lo que pasa cuando se alcanza la
catástrofe mathusiana, asumiendo que los recursos limitantes son renovables de
manera continua.
1
2
La primera aplicación directa de las matemáticas ocurrió a
finales del siglo XVIII con la publicación del trabajo de Thomas Malthus llamado “Un ensayo sobre el principio de las
poblaciones” (Malthus, 1798). Décadas más tarde Pierre
François Verhulst desarrolló aún más el modelo para simular los fenómenos de
estabilidad que se observan realmente en un sistema ecológico en su publicación
llamada “Notice sur la loi que la population suit dans son accroissement”
que más o menos traduce como “sobre las leyes del crecimiento de las
poblaciones” (Verhulst, 1838), este modelo es el que
conocemos como la curva logística exponencial, sin embargo pasarían casi
90 años hasta que estas ecuaciones fueran modificadas para crear modelos
nuevos.
El impacto de
Malthus fue más evidente, en parte a que era inglés y es probable que
fuera leído por los naturalistas ingleses, quienes eran los más importantes de
la época, especialmente por Charles Darwin. En cuanto a Verhulst, era francés y
los ingleses probablemente no estaban en buenos términos por aquel entonces.
Otra explicación es que al igual que le sucedió a Gregor Mendel, la
matematización de historia natural era aún un concepto mal visto por muchos
naturalistas en la época, por lo que habría que esperar hasta que las
matemáticas irrumpieran en la genética, y así la historia natural se transformaran
en una ciencia, que al igual que la física encontraba su sustento principal en
modelos matemáticos de situaciones ideales que aun así permitían responder
preguntas sobre situaciones reales.
Los primeros modelos matemáticos modernos fueron ofrecidos
por Alfred Lotka, Vito volterra y andrei Andréi Kolmogórov. Este primer
modelo es conocido simplemente como el modelo Lotka-Volterra Depredador-Presa,
aunque no es que los dos hubieran trabajado simultáneamente en el asunto.
Alfred J. Lotka lo propuso inicialmente como parte de una teoría de reacciones
autocatalíticas en 1910 (Lotka, 1910), de hecho se trataba de una
situación en la que se tenía dos poblaciones creciendo simultáneamente
modelados por medio de la curva logística de Verhulst con operadores extra
necesarios para representar los efectos de la interacción depredador presa. En 1920 Lotka extendió las
ecuaciones a sistemas orgánicos influido por el trabajo de Andrei Kolmogorov
tomando como ejemplos biológicos la relación de forrajeo (Lotka, 1920) y la relación de depredadores
y presas (Lotka, 1925). Las mismas ecuaciones fueron
publicadas independientemente por Vito Volterra en 1926, él era un matemático y
físico que se interesó en modelar situaciones biológicas gracias al trabajo de
su Yerno sobre la abundancia de peces depredadores en el mar Adriático justo después de la
Primera Guerra Mundial (1914-1918), con los datos de su yerno, Volterra fue
capaz de desarrollar el modelo de depredadores y presas (Goel, Maitra, &
Montroll, 1971; Volterra, 1927, 1928)
En 1936 Andreui Kolmogorov extendió el modelo Lotka-Volterra
más allá de las relaciones depredador-presa a otras relaciones ecológicas, como
los mutualismos y la competencia interespecífica (Kolmogorov, 1936; May
& Leonard, 1975).
Las ecuaciones de Lotka-Volterra tienen una larga historia en teoría económica.
El primero que las aplicó para la economía fue Richard Goodwin en 1965 (Gandolfo, 2008), después de todo las
industrias pueden modelarse como depredadores que deben consumir materias
primas que son limitadas, y por las cuales deben competir con industrias con
nichos económicos similares, lo cual es una relación completamente análoga a lo
que sucede en un ecosistema.
Con los años, han surgido otros modelos, uno que
posiblemente ha sido más exitoso a la hora de hacer predicciones ha sido el de
densidades dependientes del crecimiento poblacional de la presa desarrollado
por C. S. Holling, M. L. Rosenzweig y R. H. McArthur (Fussmann & Blasius,
2005; Rosenzweig & MacArthur, 1963; Wang, Fan, & Wang, 2003), aunque en la actualidad es
conocido como el modelo de respuesta funcional dependiente de radio
depredador-presa. En la actualidad estos son los dos modelos que se exponen en
los textos de enseñanza de la ecología. Posteriormente Arditi-Ginzburg modificaron el modelo para acercarlo a situiaciones mas
reales, con el costo de hacerlo más complejo (Akcakaya, Arditi, & Ginzburg, 1995;
Arditi & Ginzburg, 1989, 2012).
Aunque mucho podría indagarse sobre la matematización de la
ecología por parte de matemáticos como Volterra o Kolmogorov, por el momento
nos enfocaremos exclusivamente a una serie de conclusiones muy sencillas. Este
dialogo empieza por las funciones que nos sirven para describir la densidad
poblacional, es decir, el modelo exponencial y el modelo logístico exponencial.
Recordando la matemática de poblaciones, tenemos que el modelo logístico
exponencial es el que mejor se adecua a los problemas de los sistemas reales,
en especial los recursos limitados que provocan que las poblaciones no puedan
crecer a un nivel infinito. Ecuación logística exponencial, tasa de cambio de la ecuación logística exponencial y gráfica
de la función logística exponencial Figura 54.
Gráfica de la forma integrada del modelo
logístico exponencial, es una gráfica bastante típica con forma sigmoide
"s", la cual se puede describir en cuatro fases, la primera fase es
la de crecimiento logarítmico y es muy lenta, representa el momento en que una
población pequeña se adecua a su ambiente; posteriormente la fase exponencial
que se caracteriza por rápido crecimiento, luego está la fase de frenado en que
la población empieza a reproducirse con más lentitud. Finalmente, la población
alcanza el límite o capacidad de carga de un sistema.
Retomando las fórmulas de crecimiento logístico tendríamos
que dos especies independientes que deberán modelarse en una misma fórmula
podrán ser expresadas del siguiente modo.
3
4
Básicamente todas las variables les agregamos un subíndice
para identificar cuando estamos trabajando con una especie u otra en la pareja
de competidores a y b. En estos modelos el crecimiento
poblacional disminuye a medida que el tamaño de la población aumenta hasta
llegar a la capacidad de carga K. La presunción básica del modelo
logístico es básicamente el efecto de la competencia intraespecífica, sin
embargo, para modelar la competencia interespecífica se requieren de operadores
matemáticos más complejos, que de cierta forma son formulados por matemáticos,
los ecólogos como tal se encargan de corroborar o refutar los modelos en el
campo. Para nuestro caso en particular la pareja de fórmulas Lotka-Volterra son
las siguientes.
5
6
En este segundo caso la capacidad de carga se alcanza más
rápido ya que el consumo de recursos es realizado por los individuos de la
especie más los individuos de la especie competidora multiplicado por un factor
de sobrelapado de nicho alfa (αab/αba).
El alfa nos indica que tan sobrelapantes son los nichos de las dos especies,
por lo que, a mayor valor, entonces las especies tienden a ser más semejantes,
y requieren más de los mismos recursos. Formalmente el alfa se denomina
coeficiente de competencia. En términos prácticos el efecto de la competencia
es la disminución de la capacidad de carga real del ecosistema para las
especies en competencia, por lo que solo puede haber menos individuos de los
posibles, so pena de activar los mecanismos de control de poblaciones como la
limitación de recursos “hambruna”, los depredadores y los parásitos asesinos.
Matemáticamente debido a que las dos especies técnicamente operan como una sola
metaespecie cuando se alcanza el equilibrio solo hay dos resultados posibles,
el primero y matemáticamente más probable es que una de las especies excluya a
la otra al tener mejores capacidades de supervivencia. El segundo caso es que
ambos alcancen un equilibrio no cíclico.
Ahora bien, las ecuaciones Lotka-Volterra depredador-presa
nos permite graficar el cambio de las poblaciones de dos especies A y B a lo
largo del tiempo, donde ambas gráficas se encuentran vinculadas entre sí
mediante una interacción ecológica, como la depredación. Así, al adicionar un
modificador a la ecuación logística y vincular dos de estas ecuaciones para
cada una de las especies se obtiene el modelo que generalmente es reconocido en
la literatura como el modelo Lotka-Volterra de depredadores y presas. Si se
tienen dos especies a las cuales llamaremos a y b, se tiene que una especie
causa un efecto negativo en la otra, mientras que la relación inversa es
positiva. Adicionalmente, ambas especies crecen de una manera logística
exponencial. Al igual que sucede con la logística, las ecuaciones L-V se
expresan generalmente en términos de su tasa de cambio “derivada” no en
términos de sus valores absolutos “integrada”. La ecuación Lotka-Volterra
modela a las presas como anfitriones y hospederos ya que son ellos quienes
ofrecen los recursos para que el depredador pueda sobrevivir:
7
El modelo Lotka-Volerra para la presa no tiene en cuenta la
capacidad de carga debido a que las muertes del depredador “hunter” h se
dan mucho antes de alcanzar su capacidad de carga, dichas muertes se modelan
mediante el factor ρ multiplicado por las poblaciones del depredador Nh
y la presa Np. En este factor el término ρ significa
la tasa de depredación, aumentando si el depredador es muy efectivo y
disminuyendo si la presa puede defenderse exitosamente. Por el otro lado de la
relación obtenemos lo siguiente:
8
En este caso el operador cρ indica la tasa con la
cual la biomasa de la presa es convertida en nuevos depredadores. El segundo
término es la tasa de muertes del depredador que posee un valor de
decrecimiento intrínseco. En el modelo clásico de Lotka-Volterra todos los
operadores que no son tamaño de poblaciones son constantes, sin embargo, en la
naturaleza estos valores cambian constantemente. Al integrar y resolver ambas
funciones “formas integradas del modelo de Lotka-Volterra que es verdaderamente
difícil de encontrar en los textos de introducción a la ecología matematizada”
se nos genera una gráfica muy particular.
Figura 55. Oscilación Lotka-Volterra. Gráfica de
población del cazador “hunter” Nh y de la presa “prey” Np
con respecto al tiempo t.
La gráfica del modelo L-V es típico, asemejándose a una
gráfica simultánea del sen x y cos x, en este caso la población
de presas al llegar a un punto interior a la capacidad de carga es abrumada por
la población de depredadores, pero cuando las presas se hacen menos comunes,
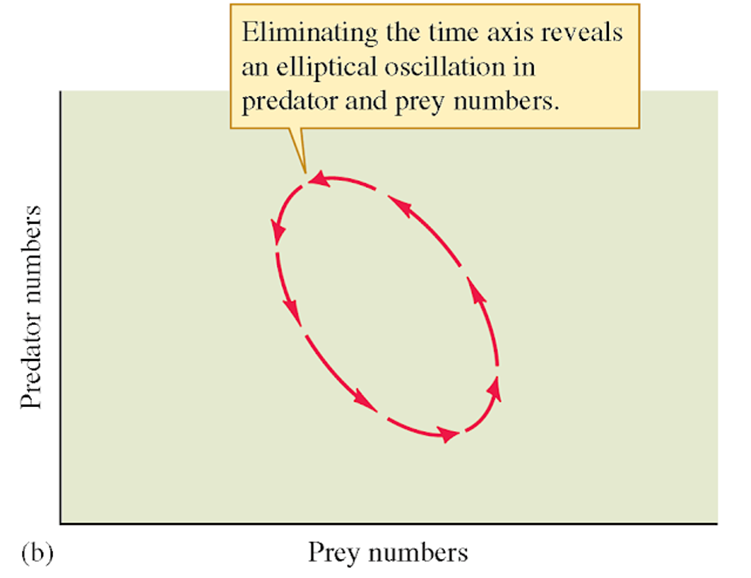
los depredadores también sufren. La relación depredador-presa se puede
identificar más fácilmente si se elimina el eje tiempo, y en la gráfica solo
delineamos las variables poblacionales del depredador y de la presa.
Se puede observar que el cambio en la población de presas es acompañado por un cambio en la población de depredadores similar, pero desfasado en el tiempo, operando dentro de un rango de valores, es decir, dentro de un equilibrio dinámico. Lo que sucede con las presas afecta a los depredadores a largo plazo, y un desequilibrio en la población de cualquiera de los dos afecta a su compañero. Por otro lado, la gráfica de la relación L-V no solo arroja un equilibrio dinámico, en ocasiones se pueden presentar equilibrios inestables, o equilibrios estabilizantes Figura 57.
Figura 56. Equilibrio dinámico estable. Gráfica de Nh contra Np, donde se muestra la naturaleza cíclica teórica de dos poblaciones de depredador y presa.
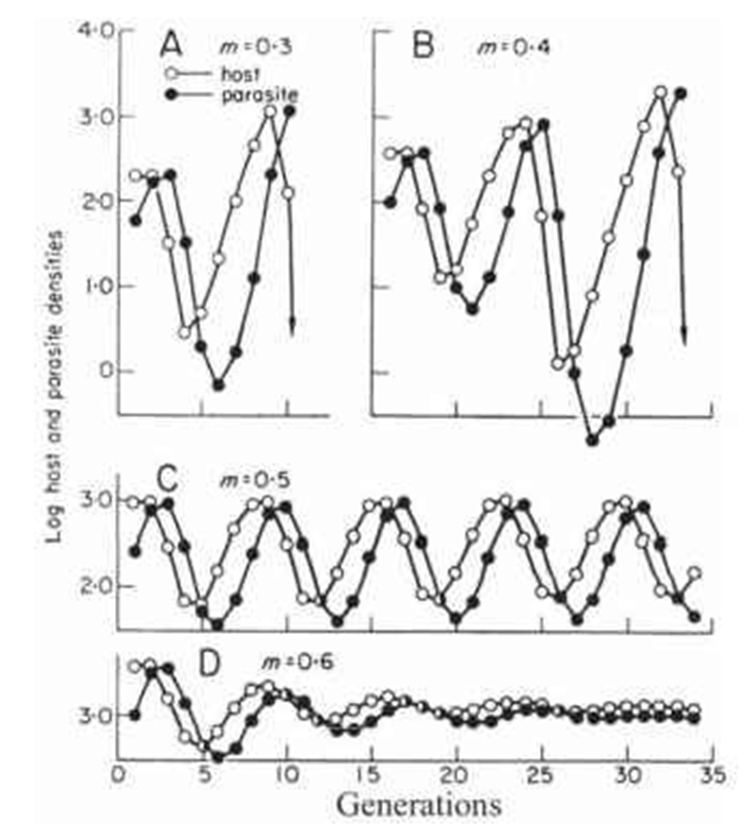
Figura 57. Oscilaciones estables e
inestables. En la realidad los ciclos de Lotka-Volterra no son estables, y
puede haber extinciones.
Las oscilaciones en el modelo LV son diferentes dependiendo
del sistema, en A y B Figura 57
tenemos equilibrios muy inestables, de hecho, en B la población de parásitos se
extinguió en ese sistema, por lo que una nueva población inicial debió haber
reingresado desde sistemas adyacentes. En C Figura 57
tenemos un equilibrio estable, aunque sus oscilaciones son peligrosamente altas
en términos del número de individuos, mientras que en D Figura 57
tenemos un equilibrio que tiende a la estabilización de ambas poblaciones.
Resulta notable que el modelo de depredador presa también pueda aplicarse a la
relación de simbiosis parasítica. es probable que D represente la evolución de
un parasitoide que mata a su hospedero a un parásito que no necesariamente lo
mata, hasta un comensal que no afecta la población del hospedero. Sin embargo,
este fenómeno no se observa de manera tan clara en la naturaleza debido a que
los depredadores tienen más de una presa a la cual cazar. Cuando una presa se
hace muy común es fácil cazarla, pero cuando su población desciende, es más
fácil cazar otras especies, esto le da la oportunidad a la primera población de
presas de recuperar sus números de individuos sin que su población tenga que
disminuir de una manera tan drástica.
Con tan solo adicionar una tercera especie, otra presa
tenemos un efecto de amortiguamiento de la depredación en la población de
presas “en ingles se usa con frecuencia el nombre de buffer al efecto de
amortiguamiento”.
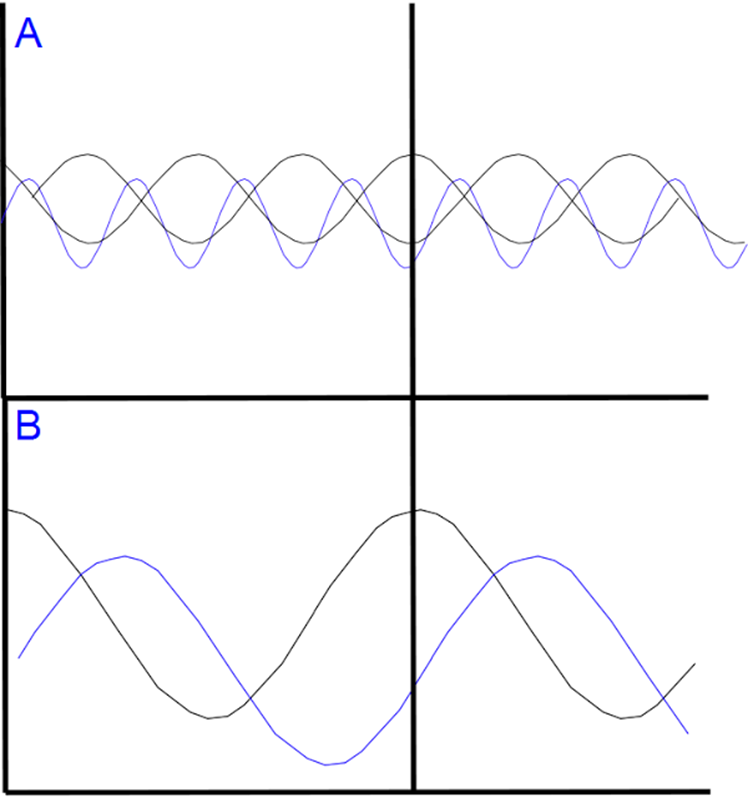
En la Figura 58 tenemos en B una relación entre un depredador y una presa, sus oscilaciones son más amplias ya que con una sola presa, esta enfrenta más presión del depredador, por lo que tarda más tiempo en regenerar su población. Lo mismo para el depredador, mientras más difícil es encontrar la presa, sus números se mantienen ambos por más tiempo. En A tenemos un modelo con dos presas, que permite el mantenimiento de un equilibrio menos inestable, ya que el depredador puede alternar entre una presa y otra a medida que una población decrece y otra aumenta.
Figura 58. Número de especies y estabilidad. Ciclos LV entre un depredador y dos presas (A) y un depredador y
una presa (B). Los ciclos de más de dos presas son más estables.
Lo anterior implica que, los números para la cantidad de
individuos de cada especie variaran en una comunidad como función del número de
especies, así entre mayor es el número de especies en una comunidad, menor es
la oscilación de las poblaciones, lo que hace que la comunidad sea más estable
y tenga menores riesgos de generar una extinción espontánea. Las comunidades ecológicas con menor número
de especies tienden a tener una mayor variación en su número de individuos, lo
cual puede provocar riesgos de extinciones locales o globales de una especie o
grupos de especies interrelacionadas.
El modelo clásico de Lotka-Volterra-Kolgomorov ha estimulado
una enorme investigación tanto en el campo como a nivel teórico-matemático
desde su publicación y maduración a lo largo del siglo XX. La utilidad de dicho
modelo emerge de su simplicidad lo cual es la característica principal de
cualquier ley científica. Sin embargo, como se ha mencionado anteriormente,
esta simplicidad aparece al asumir ciertas situaciones que biológicamente son
irreales. Una de estas presunciones es que la tasa con la que un depredador
individual consume a la presa está determinada únicamente por la abundancia de
la presa. En este modelo el tamaño de la población del depredador no afecta la
tasa de depredación como tal “aunque si afecta la población de la presa”. Otra
presunción es que la conversión de biomasa de la presa a nuevos depredadores es
un proceso instantáneo, lo cual en la realidad puede presentar periodos de
retardo muy prolongados, especialmente en depredadores grandes que requieren
más de un ciclo anual para cazar por su mismos. Estas presunciones pueden
justificarse en modelos donde el depredador tiene muy bajas densidades poblacionales
o donde sus ciclos de vida son muy cortos. Pero en otros casos, es necesario
realizar otro procedimiento matemático. El modelo de Holling ilustrado bajo la
notación de Arditi y Ginzburg es el siguiente:
9
Donde gN es la tasa con la que la presa es
consumida por el depredador, a es la eficacia de búsqueda del depredador, h
es el tiempo de cacería para una presa particular ya que algunas son más
fáciles de cazar que otras y N es la abundancia absoluta de la presa en
un momento de tiempo determinado. En este modelo aun cuando la presa llega a
sus valores de capacidad de carga, el depredador no mejora su eficacia debido a
que tiene tiempos para cazar y limites en su eficacia de cacería. Posteriormente Arditi y Ginzburg
propusieron un mejoramiento del modelo, aduciendo que la tasa de consume de la
presa es afectado no por la cantidad absoluta de presas, sino por su cantidad
relativa con respecto al depredador, concepto conocido como el radio de
depredadores y presas, lo cual se modela como un valor fraccionario.
10
En el modelo Arditi-Ginzburg a no es el tiempo de búsqueda,
sino la tasa con que la presa se hace accesible al depredador por cualquier
mecanismo, lo cual incluye el efecto de los parásitos o la edad, no solo la
capacidad para caza, y h sigue siendo el tiempo de cacería.






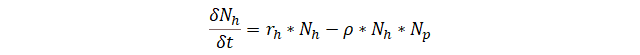
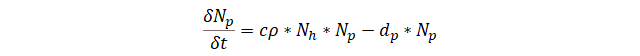




No hay comentarios:
Publicar un comentario