(Ciencias de Joseleg)(Biología) (Ecología) (La población) (Introducción) (Generalidades) (Historia) (Características) (Patrones de supervivencia y distribución de edades) (Crecimiento lineal y geométrico) (Crecimiento exponencial) (Crecimiento logístico) (Interacciones intraespecíficas) (Referencias bibliográficas)
Aunque normalmente decimos que la biología nace de los trabajos independientes de Gregor Mendel sobre la matematización de la variabilidad y la herencia y de Darwin sobre la selección natural, ambos durante la primera mitad del siglo XIX, sería más justo argumentar que el ingreso de la historia natural al mundo matemático y por lo tanto, su configuración como una ciencia moderna al estilo de la física fue un proceso mucho más gradual que antecedió a Darwin y Mendel y que prosiguió mucho después de ellos (Bizzo & El-Hani, 2009; Edwards, 2016; Jost, 2015; Knippels, 2002), el uso de las matemáticas en la biología puede rastrearse hasta 1798 con los trabajos de Thomas Malthus "imagen siguiente" sobre el comportamiento de una población de organismos (Malthus, 1809, 1798). Evidentemente el modo en que ingresan las matemáticas a la biología es un poco más tortuoso, ya que no sería aceptado generalizadamente sino hasta la llegada del siglo XX cuando el proyecto de la genética inicia fuertemente (Fowler & Kuebler, 2014; Gunawardena, 2013; May, 2004).
Sin embargo, nos concentraremos en este capítulo en cómo se
desarrollaron los primeros principios de la ecología de poblaciones, los
modelos de crecimiento, ya que los modelos matemáticos de crecimiento
poblacional son fundamentales para poder entender a la teoría más importante de
la biología, la Teoría de la Evolución. En este capítulo en concreto nos
enfocaremos en la historia y las definiciones, mientras que en capítulos
siguientes nos enfocaremos en sus matemáticas y consecuencias a largo plazo.
La matematización de Mendel no es un esfuerzo aislado al
interior de la biología del siglo XIX. Con la introducción de las gráficas de
poblaciones contra tiempo atribuidas a Thomas Malthus “1766-1834” la dinámica
de las poblaciones se ha convertido en la rama por excelencia de la biología
matematizada (Allen, Jang, & Roeger, 2017; Cohen, 1995; Wei, Jiang, &
Zhang, 2015). El primer principio de la dinámica de poblaciones es la bien
conocida ley de crecimiento exponencial de Malthus postulada en el siglo XIX y
que sirvió como fundamento seminal para los pensamientos de Darwin
"1809-1882" y Wallace "1823-1913"; y que concluyeron con el
enunciado con el principio de la selección natural (Beachly, 2010;
Klimek, 2009; Neal, 2004). Otros autores importantes en el ramo del estudio de
la demografía fueron los realizados por Benjamin Gompertz “1779-1865” y Pierre
François Verhulst “1804-1849”, los cuales ajustaron y expandieron los trabajos
de Malthus (Anderson, 2010; Iliev, Kyurkchiev, & Markov, 2015; Kucharavy
& De Guio, 2011a, 2011a, 2011b; Marmet, 2014).
El modelo Lotka-Volterra propuesto entre 1925 y 1926
independientemente por Alfred J. Lotka “1880-1949” y Vito Volterra “1860-1940”
son otro caso de un famoso grupo de ecuaciones que presentan una amplia
aplicación en sistemas simulados (Berryman, 1992; Takeuchi, 1996; Wangersky,
1978), como por ejemplo en juegos como Simsity, Ultima Online (Collet, 2007;
Landriscina, 2013; Squire & Patterson, 2010; Whitkin, 2013), en los que es
un requisito indispensable poder simular el comportamiento de las poblaciones.
La dinámica de poblaciones ha convergido de dos formas con la teoría evolutiva,
la primera vez cerca de la década de 1910-1920 lo que conllevó a la formulación
la genética de poblaciones y la segunda en los últimos 30 años con la
introducción de la teoría de juegos evolutivos desarrollada por John Maynard
Smith “1920-2004” (Hammerstein & Selten, 1994; Maynard-Smith, 1978, 1984,
1989).
El fundamento de la razón es la capacidad de realizar
juicios basados en otros juicios previos, esto implica la necesidad de generar
conexiones de causa y efecto entre dos variables. Uno de los objetivos de las
ciencias de la naturaleza es la necesidad de encontrar patrones que generan esa
conexión entre dos variables aparentemente independientes y que nos permiten
conocer y predecir ciertas propiedades del sistema de estudio. Como se
mencionó previamente, los ecólogos de poblaciones desean entender los procesos
generales al interior de poblaciones de seres vivos, sin importar si hablamos
de bacterias, de pastos o de lobos basados en un proceso de reducción de
variables y matematización; es decir mediante una aproximación de tradición
fiscalista.
De hecho, el mismo nombre de dinámica es una analogía con el
estudio de la dinámica en física, y mucho de ese lenguaje es trasladado, como
los conceptos de velocidad promedio, velocidad instantánea, tasa de
crecimiento, aceleración, simbologías para el cambio como los deltas entre
otros. Por lo anterior podemos definir con claridad el objetivo de la dinámica
de poblaciones como un estudio de tradición reduccionista que busca encontrar
patrones numéricos en el comportamiento de las poblaciones que puedan ser
expresadas en términos de ecuaciones matemáticas simples.
Thomas Malhus “1766-1834” fue un clérigo ingles famoso por
sus opiniones políticamente incorrectas sobre las ayudas sociales a los más
necesitados, aunque en cualquier caso su aproximación al problema vale la
pena ser evaluada ya que se convertiría en el fundamento seminal del cual el
estudio de la dinámica de poblaciones seria fundada. Malthus saltó a la
prominencia debido a su ensayo de 1798 titulado “Sobre el Crecimiento de las
Poblaciones”. En este escrito Malthus argumentaba que las poblaciones crecen a
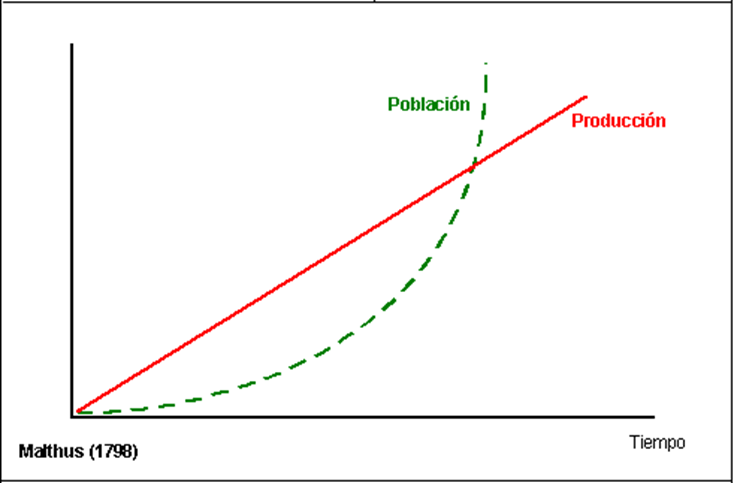
un ritmo mucho más acelerado que los recursos que las mantienen.
Figura 3. Modelo
exponencial simple. La población (línea verde) se expande más rápido
que los recursos de los que depende (línea roja), siempre que la población esté
debajo de la línea de limite, esta puede expandirse, pero llegada al punto de
pobreza, comienza la lucha por la existencia.
En términos malthusianos decía que: las poblaciones crecen
geométricamente mientras que los recursos lo hacen aritméticamente. Básicamente
una población que crece en base al modelo exponencial no puede mantener su
ritmo de expansión de forma ilimitada, por el contrario, llega a un punto donde
la disponibilidad de recursos como los alimentos limitan su crecimiento. Entre
1798 y 1826 Malthus publicó 6 ediciones de su ensayo adicionando nueva
información y respondiendo a las críticas realizadas.
Las ideas de Malthus eran revolucionarias en el sentido de
que iban en contra de las nociones y valores culturales de la época. Después de
que la revolución científica de la edad de la ilustración tomó vuelo, y su
impacto en la tecnología convirtió a Europa en la reina del mundo, la sociedad
cambió. Los europeos y en especial aquellos pertenecientes a las naciones que
procedieron a industrializarse rápidamente empezaron a valorar el futuro en
términos de un desarrollo infinito, de una mejora sin pausa, de una acumulación
hacia un desarrollo imparable. Este positivismo sobre el futuro fue defendido
por muchos académicos del siglo XVIII y XIX entre los que hay que destacar al
padre de Thomas Malthus y a otros miembros de su círculo intelectual entre los
que hay que destacar a Russeau "1712-1778", un filósofo francés muy
influyente quien veía a la naturaleza humana de forma positiva.
Los escritos de Malthus iban en directa oposición a esta
sensación de optimismo general ya que planteaba la existencia de limitantes
naturales al crecimiento de las poblaciones humanas, y entre sus críticos se
pueden resaltar William Godwin “1756-1836” y el Marqués de Condorcet
“1743-1794” (Hale, 2014; Himmelfarb, 1980; Kingsland, 1988; Waterman, 1991; Robert
Maxwell Young, 2005). Es importante resaltar que la propuesta malthusiana
original parecía limitarse específicamente a las poblaciones humanas, y que las
conclusiones que el extrajo de estas no serían bien vistas ni por su comunidad,
ni por nuestra comunidad y tampoco por este humilde escritor.
Como se mencionó anteriormente, debido a que los escritos de
Malthus iban en contra de los valores de su propia cultura levantaron una
enorme controversia y un fuerte debate, la cual ha sido denominada como la
Controversia Malthusiana (Bowen, 1817; Claeys, 2000; Robert M Young, 1969).
Como clérigo Malthus empleó sus ideas para construir un esquema moralizante, y
lo explicaremos del siguiente modo. Una población que se expande exponencialmente
consumiendo recursos que se expanden linealmente siempre llega a un punto donde
el alimento es insuficiente para todos causando un estado de tensión social,
pobreza y hambruna. Malthus culpaba de este estado “en las poblaciones humanas”
a la gran tasa reproductiva, es decir a la generación de mucha descendencia por
parte de las familias, especialmente las más pobres. De este modo las familias
pobres deberían regular la tasa de natalidad o de lo contrario verían a sus
hijos más débiles morir de hambre naturalmente.
Malthus enfatizó la existencia de dos puntos de regulación de la población, unos positivos y otros preventivos. La regulación positiva sobre la población eran todas aquellas acciones o fenómenos que se desencadenaban por la alta población y que la regulaban de forma muy directa, se pueden citar en este sentido a la hambruna, la enfermedad y la guerra. La regulación preventiva se relacionaba con aquellos fenómenos que regulaban la tasa de natalidad y por lo tanto disminuían los riesgos de que la regulación positiva fuera activada. Entre la regulación preventiva se pueden citar al aborto, el control de la natalidad, la prostitución, el celibato y el matrimonio a edades más altas. Malthus argumentó que de todos los mecanismos de limitación eran preferibles los preventivos, y de todos ellos los que eran moralmente válidos como el celibato y el matrimonio a edades más altas, esto conllevaría a una mejora en las condiciones de vida de los individuos, incluyendo los ambientes en los cuales los descendientes sería educados.
Figura 4. Crecimiento poblacional
humano. La población humana a lo largo de las eras se ha mantenido bajo
control, pero con la revolución industrial y científica, la especie humana se
ha multiplicado.
En 1798, Thomas Malthus escribió: “el poder de la población
es tan superior al poder de la Tierra para producir los medios de subsistencia
para el hombre, que la muerte prematura visitará de una forma o de otra a la
raza humana. Los vicios de la humanidad son activos y son ministros de la
muerte. Ellos son los próceres en el ejército de la destrucción, y son capaces
de terminar su aterrador trabajo por sí mismos” (Malthus, 1798b; Smail, 2003).
Malthus hace referencia a que las estaciones duras, las epidemias, la
pestilencia, la plaga, la guerra, aunque bloquean el crecimiento de las
poblaciones son insuficientes y que a final de cuentas lo que limita las
poblaciones es la hambruna. Aunque puede sonar más a una profecía
apocalíptica que a una predicción matemática, Malthus no parecía estar muy
preocupado, ya que en realidad tenía confianza en que los mecanismos de
regulación preventivos y algunos positivos evitarían la destrucción completa de
la sociedad (Documental: Último aviso-Los límites del
crecimiento.).
Muchas de las críticas al trabajo de Malthus han provenido
desde el campo de la economía, sobre todo aplicado a las poblaciones humanas.
Escritores como Ester Boserup “1910-1999” (Grigg, 1979), Julian Simon
“1932-1998” (Ahlburg, 1998); Henry George "1839-1897" (Figueras &
Morero, 2012; Horner, 1997) e incluso Friedrich Engels "1820-1895"
(Anderson, 2010; Kelley & Williamson, 1984) criticaron el trabajo de
Malthus en base a criterios económicos de desarrollo tecnológico y científico.
El argumento general es que una vez que una población empieza a alcanzar los
límites de recursos, el trabajo de los científicos y su aplicación tecnología
permite el desarrollo de nuevos métodos agrícolas que incrementan la producción
de alimento, lo cual permite un incremento de la población hacia nuevos
límites. En parte este argumento ha sido valido ya que después de Malthus las
mejores en la tecnología agrícola y médica hicieron que la población humana se
disparara de forma violenta como se ve en la siguiente gráfica. Desde los primeros registros humanos hasta
casi el siglo XVIII la población humana creció levemente y de forma estable
hasta que la edad industrial y científica permitió retirar los bloqueos que
existían sobre las poblaciones, especialmente el hambre y la peste, porque la
guerra ha seguido con nosotros y parece no controlar nuestros números.
Sin embargo, la mejora científica no se puede dar de forma
infinita, no es magia, y las tecnologías y ciencias agrícolas siempre tienen en
cuenta que se basan en sistemas reales con limitaciones. Actualmente es cada
vez más costoso y difícil el desarrollo de nuevas tecnologías para la mejora
agrícola y médica, por lo que en últimas la solución aplicada es la antigüita,
expandir la frontera agrícola y depredar el medio ambiente.
La frontera agrícola es el límite entre los sistemas intervenidos de forma dura para la agricultura y los sistemas que interactúan con el hombre, pero mantienen cierto nivel de naturalidad. A medida que la presión alimentaria se incrementa y la falta de tecnología se hace evidente, la única opción es derribar zonas naturales para cultivar o criar ganado. Muchos de los problemas ambientales en la actualidad, “por no decir que TODOS según autores como Cristian de Duve” se deben precisamente en ese exceso de confianza en un avance científico ilimitado por quienes no saben nada de ciencias de la naturaleza, pero que sin embargo tienen los cargos de decisión sobre políticas de estado (Chellaney, 2013; De Duve & Pizano, 1995; Kadin, 2014; M. R. Mason, 2015; Strydom & Struweg, 2016).
Figura 5. La
frontera agrícola. La expansión de la frontera agrícola es una tendencia
natural, realizada ya sea por grandes corporaciones, gobiernos o por personas
pobres que buscan crear un terruño propio.
La destrucción se las selvas (Bergius, Benjaminsen, &
Widgren, 2017), la contaminación de los ríos, la destrucción de la capa de
ozono y la polución de aire (Gray, 2015; Hadfield, 2016; Ruhil, 2016) son
causadas por tecnología anticuada que sustenta una población simplemente
demasiado grande y que se expande a demasiada velocidad. Un ejemplo simple nos
lo da la ruta entre el poblado del departamento de Cundinamarca llamado Madrid
y el casco urbano de la ciudad de Bogotá en Colombia, esta zona había sido
usada hasta hace poco para la producción agrícola, pero la presión poblacional
de la ciudad de Bogotá presiona y expande sus límites, por lo que estos
territorios están siendo empleados para la construcción de conjuntos
residenciales.
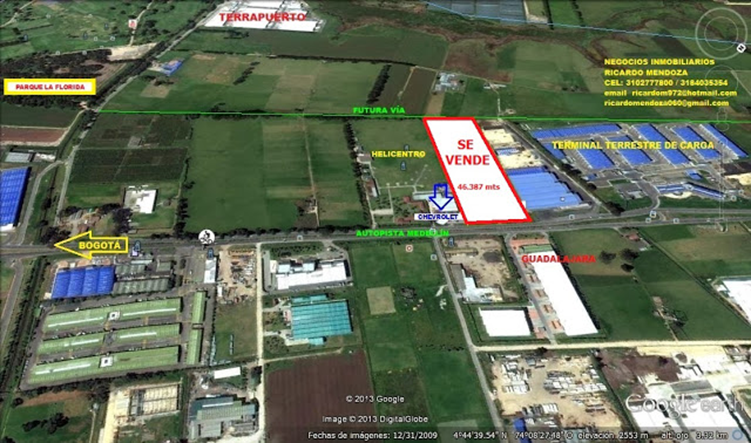
Figura 6. Fragmento
de la vía Bogotá Madrid. Como puede verse el trazado de la zona delata su
uso tradicional como productora agrícola cercana a la ciudad, sin embargo, se
encuentra bajo una fuerte presión hacia la urbanización. ¿Si construimos sobre
lo que comemos, que vamos a comer?
Si comenzáramos con una sola bacteria de Escherichia coli,
y asumiendo que la división celular se da cada 30 minutos, le tomaría menos de
una semana a sus descendientes exceder la masa del planeta Tierra. Obviamente,
la expansión exponencial no es un fenómeno restringido a las bacterias. O como
lo diría el señor Jacques Monod, “Aquello que es válido para E coli,
también lo es para los elefantes”, por supuesto, el propio Darwin usó a los
elefantes como una ilustración del principio de rápido crecimiento poblacional.
Calculando, que el número de descendientes de un solo par de elefantes podría
conllevar a más de 19 000 000 en solo 750 años. Una pareja de ostras tiene la
capacidad de producir más de 114 000 000 huevos en tan solo una puesta, lo que
implicaría que, si todos sobrevivieran, en tan solo 5 generaciones, se
generarían más individuos que electrones en el universo.
Resulta obvio que el universo, la galaxia, el sistema solar
o el planeta Tierra no se encuentran saturados ni de elefantes, ostras o
bacterias. El hecho de que estas especies y de hecho todos los seres vivos del planeta
posean una capacidad de masiva reproducción o (superfecundidad), y que por lo
tanto pudiesen en principio expandirse exponencialmente sin límite alguno, no
se transfiere en la práctica, donde todos los seres vivos en condiciones
normales mantienen un nivel de población estable, aunque dinámico. Esto genera
más preguntas, ¿Qué mantiene limitadas a las poblaciones? Y si la limitación de
las poblaciones implica la muerte de enormes cantidades de individuos por cada
generación, ¿Quiénes son los que sobreviven?, ¿Quiénes sobreviven lo hacen al
azar o existen otros fenómenos que los seleccionan?
Figura 7. Modelos de
crecimiento más conocidos. (Izquierda) modelo exponencial simple de Malthus;
(Derecha) modelo de crecimiento logístico de Verhulst.
Todos los seres vivos poseen la propiedad de
superfecundidad, desde la ballena que se reproduce más lentamente hasta la
bacteria que se duplica cada 20 minutos. Sin embargo, la superfecundidad no es
compatible con un sistema real cuyos recursos son limitados. Es por esto
que el modelo exponencial simple no puede decirnos que sucede una vez que los
recursos se hacen limitados. En esta serie de artículos nos enfocaremos en el
modelo matemático del crecimiento logístico exponencial, y como sus
consecuencias permiten realizar la deducción de un proceso vital en la
evolución de los seres vivos, la selección natural.
El modelo logístico exponencial fue planteado originalmente
por Pierre François Verhulst “1804-1849” en el año de 1838 (Bacaër, 2011;
Berryman, 1992; Cramer, 2002). La expresión matemática genera una curva
sigmoidea, es decir en forma de S en lugar del crecimiento exponencial simple
que tiene forma de J. En este modelo Verhulst propuso que el crecimiento de la
población estaría limitado por la disponibilidad de recursos en un territorio
determinado. Si les suena al planteamiento malthusiano no es coincidencia,
Verhulst leyó primero las consecuencias del crecimiento exponencial en el
ensayo original de Malthus, y luego realizó la corrección del modelo para que
se ajustara de una mejor forma a las realidades. Cabe anotar que la ecuación
que genera el modelo volvió a ser planteada por Alfred J. Lotka
"1880-1949" en 1920 denominándola ley del crecimiento poblacional
(Volterra, 1928; Wangersky, 1978).
El impacto de Malthus fue más evidente, en parte a que era
inglés y es probable que fuera leído por los naturalistas ingleses, quienes
eran los más importantes de la época, especialmente por Charles Darwin. En
cuanto a Verhulst, era francés y los ingleses probablemente no estaban en
buenos términos por aquel entonces. Otra explicación es que al igual que le
sucedió a Gregor Mendel, la matematización de historia natural era aún un
concepto mal visto por muchos naturalistas en la época, por lo que habría que
esperar hasta que las matemáticas irrumpieran en la genética, y así la historia
natural se transformaran en una ciencia, que al igual que la física encontraba
su sustento principal en modelos matemáticos de situaciones ideales que, aun
así, permitían responder preguntas sobre situaciones reales.
Los primeros modelos matemáticos modernos fueron ofrecidos
por Alfred Lotka, Vito volterra y andrei Andréi Kolmogórov. Este primer modelo
es conocido simplemente como el modelo Lotka-Volterra Depredador-Presa, aunque
no es que los dos hubieran trabajado simultáneamente en el asunto. Alfred J.
Lotka lo propuso inicialmente como parte de una teoría de reacciones
autocatalíticas en 1910 (Lotka, 1910), de hecho, se trataba de una situación en
la que se tenía dos poblaciones creciendo simultáneamente modelados por medio
de la curva logística de Verhulst con operadores extra necesarios para
representar los efectos de la interacción depredador presa. En 1920 Lotka
extendió las ecuaciones a sistemas orgánicos influido por el trabajo de Andrei
Kolmogorov tomando como ejemplos biológicos la relación de forrajeo (Lotka,
1920) y la relación de depredadores y presas (Lotka, 1925).
Las mismas ecuaciones fueron publicadas independientemente
por Vito Volterra en 1926, él era un matemático y físico que se interesó en
modelar situaciones biológicas gracias al trabajo de su Yerno sobre la abundancia
de peces depredadores en el mar Adriático justo después de la Primera Guerra
Mundial (1914-1918), con los datos de su yerno, Volterra fue capaz de
desarrollar el modelo de depredadores y presas (Goel, Maitra, & Montroll,
1971; Volterra, 1927). En 1936 Andrei Kolmogorov extendió el modelo
Lotka-Volterra mas allá de las relaciones depredador-presa a otras relaciones
ecológicas, como los mutualismos y la competencia interespecífica (Kolmogorov,
1936; May & Leonard, 1975). Las ecuaciones de Lotka-Volterra tienen una
larga historia en teoría económica. El primero que las aplicó para la economía
fue Richard Goodwin en 1965 (Gandolfo, 2008), después de todo las industrias
pueden modelarse como depredadores que deben consumir materias primas que son
limitadas, y por las cuales deben competir con industrias con nichos económicos
similares, lo cual es una relación completamente análoga a lo que sucede en un
ecosistema.
Con los años, han surgido otros modelos, uno que
posiblemente ha sido más exitoso a la hora de hacer predicciones ha sido el de
densidades dependientes del crecimiento poblacional de la presa desarrollado
por C. S. Holling, M. L. Rosenzweig y R. H. McArthur (Fussmann & Blasius,
2005; Rosenzweig & MacArthur, 1963; Wang, Fan, & Wang, 2003), aunque en
la actualidad es conocido como el modelo de respuesta funcional dependiente de
radio depredador-presa. En la actualidad estos son los dos modelos que se
exponen en los textos de enseñanza de la ecología. Posteriormente
Arditi-Ginzburg modificaron el modelo para acercarlo a situaciones más reales,
con el costo de hacerlo más complejo (Akcakaya, Arditi, & Ginzburg, 1995;
Arditi & Ginzburg, 1989, 2012).
La irrupción de las matemáticas no solo involucró a los
modelos de crecimiento poblacional, sino a otras características cuantificables
de una población. En paralelo a Morgan y el estudio de la genética, Raymond
Pearl estudió las características como la tasa de natalidad, la tasa de
mortalidad y el tamaño de la población, y reconceptualizar las dinámicas genéticas
y ambientales del cambio evolutivo. Su trabajo lo llevó de diversas maneras a
un nuevo análisis de las predicciones de Malthus sobre la densidad de población
y en conflicto directo por competencia intraespecífica, con las tendencias de
investigaciones eugenésicas para centrarse en rasgos individuales y parejas
sexualmente reproductivas.
Con el tiempo se han ido adicionando nuevas características
al estudio de las poblaciones, sin embargo los esbozos básicos de los modelos
de crecimiento poblacional es lo que nos permite obtener principios
fundamentales para el comportamiento de los seres vivos, y finalmente,
justificar el comportamiento de la Selección Natural a un nivel
matemático, en otras palabras, a través de las matemáticas de la ecología y de
la genética podemos expresar la selección natural en términos de una ecuación,
no tan simple, pero igual, cumpliendo el rigor matemático de cómo se expresan
las leyes científicas.




No hay comentarios:
Publicar un comentario