(Ciencias de Joseleg)(Biología) (Ecología) (La población) (Introducción) (Generalidades) (Historia) (Características) (Patrones
de supervivencia y distribución de edades) (Crecimiento
lineal y geométrico) (Crecimiento
exponencial) (Crecimiento
logístico) (Interacciones
intraespecíficas) (Referencias
bibliográficas)
Antes de introducir el problema del crecimiento exponencial, se trabajará con el modelo matemático lineal para introducir una serie de nombres de variables que serán empleados en todos los modelos de dinámica de poblaciones. Entre ellos cabe destacar a los símbolos para el tamaño de la población, la designación del tiempo y el mucho más importante, tasa de crecimiento de la población. Aunque la tasa de crecimiento de la población y el tiempo poseen significados diferentes dependiendo del modelo a trabajar, sus significados intrínsecos son semejantes y serán trabajados con más profundidad en los siguientes artículos. El objetivo primordial no es las fórmulas matemáticas, por el contrario, es el análisis gráfico.
Figura 13. Modelo
lineal. La variable dependiente es el número total de individuos
que será simbolizado con la letra (N) mayúscula, emplearemos (n)
minúscula en caso de que estemos analizando una fracción de la población total,
como por ejemplo el número de machos, el número de crías o el número de
hembras. La suma de todos los (n) debe dar como resultado el número
total de la población (N). Por lo tanto, es posible expresar el problema en
términos de un plano cartesiano.
Ya sé que las poblaciones no crecen linealmente, pero el
modelo inicial siempre es la base de todos estos tipos de cálculos.
Dado que los modelos de crecimiento exponencial son
básicamente copias de conceptos de dinámica, se aconseja repasar lo trabajado
en el movimiento uniformemente acelerado. Sin embargo, si usted se encuentra en
educación básica introduciremos brevemente algunos conceptos y simbología
mediante la gráfica de la línea recta. Los modelos de crecimiento exponencial
son sistemas de dos variables, una independiente y la otra dependiente. La
variable independiente es el tiempo, la cual solo tiene un eje posible y es el
positivo, debido a que el tiempo siempre avanza hacia adelante. Esta variable
será simbolizada con la letra (t).
En base a la gráfica en el plano cartesiano podemos emplear
la ecuación de la recta para poder definir un concepto extra que es muy
importante en la dinámica de poblaciones y es la tasa de crecimiento de la
población. En una línea recta la tasa de crecimiento poblacional es homóloga a
la pendiente de la recta. Es decir si tenemos la ecuación de la recta podemos
reemplazarla con las variables de nuestra recta, las “Y” se reemplazan por el
tamaño de la población y las “X” por el tiempo, lo cual nos deja la ecuación expresada
del siguiente modo:
2
Tamaño poblacional en función de la tasa de crecimiento
intrínseca, el tiempo y el tamaño inicial como un modelo de línea recta.
“N(t)” representa el
tamaño de la población en cualquier momento t. La
variable “t” representa el tiempo que puede ser expresado en
segundos, minutos, días años o más. “N(t)”
representa el tamaño de la población al inicio de la medida y en ocasiones
puede ser representada como “N(0)” que se lee
como el tamaño de la población en el tiempo cero. Mientras que “m”
es la pendiente de la recta y representa la tasa de crecimiento de la recta.
Sin embargo, lo que crece no es una recta abstracta, sino una población, por lo
que generalmente se cambia “
Crecimiento neto de la población en un modelo lineal.
La fórmula para encontrar la pendiente de una recta
cualquiera (4)
nos sirve análogamente para encontrar la tasa de crecimiento en un modelo
lineal (5).
Cabe destacar que las diferencias pueden ser reemplazadas por el símbolo delta
(Δ) que simboliza la diferencia de un punto final y un punto inicial (5).
El delta representa una resta entre dos valores muy diferentes. Pero a medida
que los valores para la resta se hacen más y más cercanos, (Δ) se reemplaza por
(ẟ) que implica la existencia de una resta entre valores infinitamente cercanos
entre sí (5).
El modelo de crecimiento lineal nos otorga dos datos o fórmulas comunes a los
demás modelos de crecimiento más empleados, el exponencial y el logístico. El
primero es la tasa de cambio (5)
que se define como el cambio de la población con respecto al cambio de tiempo a
un nivel infinitesimal, y la otra es la fórmula para calcular el tamaño de la
población para cualquier momento t (3).
Sin embargo, otros modelos nos exigirán un mayor nivel matemático.
La matematización de las poblaciones debe poder representar
al organismo sin importar la especie de la que se está hablando como girasoles,
elefantes o seres humanos. Las gráficas que se manejan siempre serán de número
de individuos en el eje (Y) contra el tiempo en el eje (X).
Cuando se realiza la gráfica en un sistema lineal aparece una variable denominada
tasa de crecimiento de la población (r).
La tasa de crecimiento a escala global está regulada por dos variables, los
nacimientos por cada individuo y las muertes por cada individuo. La relación se
modelaría en base a la siguiente fórmula simple.
6
Componentes de la tasa de crecimiento intrínseca o
percápita de la población.
Donde (a) representa la tasa de
nacimientos y (b) la tasa de muertes. El
problema es que, en la realidad la fórmula es expresada en términos un valor
arbitrario de individuos, esto se hace dividiendo a y b en una
constante de individuos llamados “per cápita”. A esa constante la llamaremos pC.
En adición a las tasas de muerte y nacimiento existe otra variable que debe
tenerse en cuenta a la hora de analizar la dinámica de poblaciones y es la
dispersión. La dispersión se define como los movimientos de individuos con
respecto a las fronteras del territorio. Si los individuos salen de la frontera
la población disminuye, pero si ingresan a las fronteras la población aumenta.
La salida de individuos se denomina emigración y el ingreso se llama
inmigración. Estas dos variables también afectan a la constante r. Donde
(c) son los individuos inmigrantes y (d)
los emigrantes.
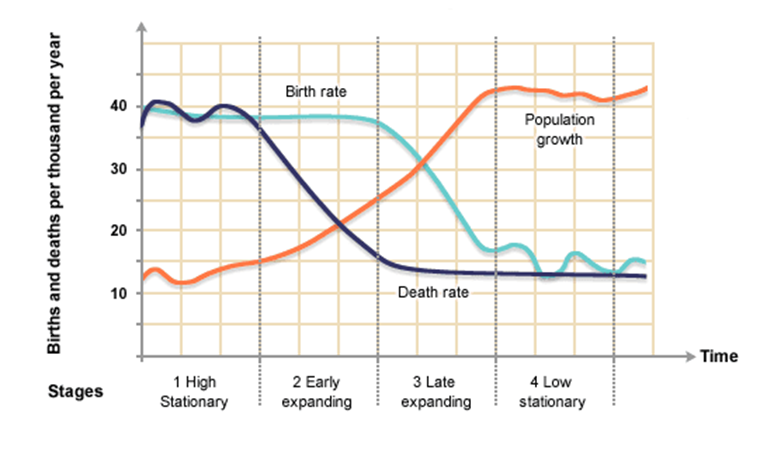
Figura 14.
Nacimientos y muertes. Gráficas de crecimiento exponencial
"naranja", tasa de nacimiento "azul claro = a" y
tasa de muerte "azul oscuro = b". La población no cambia su
tamaño cuando a = b, pero cuando hay una diferencia entre ambos
valores la población cambia. si a > b la población crece; si a < b
la población decrece.
La tasa de crecimiento intrínseca se define como la
expresión de “r” máxima, es decir cuando la
población se encuentra en condiciones ideales para su crecimiento. Estas
condiciones son la suma de los ideales de las interacciones ecológicas. Por
ejemplo, las relaciones perjudiciales como depredación, parasitismo y
competencia “interespecífica e intraespecífica” son de 0. Y las relaciones
positivas como fuentes de alimentos y recursos abióticos son óptimas. En tal
caso, la población crecerá a su máximo siguiendo un patrón exponencial mientras
que las relaciones ecológicas estén a su máximo. Las consecuencias del
crecimiento exponencial ya han sido discutidas de forma extensa mediante la
interpretación malthusiana.
El modelo geométrico se obtuvo por métodos más empíricos, consta de las variables de tamaño poblacional del modelo anterior, pero cambia la constante r por la constante λ que representa la cantidad de crías promedio de una determinada población elevado al tiempo (7).
Figura 15.
Crecimiento geométrico. El modelo geométrico modelaría una
población que crece estacionalmente, pero que no está sometida a presiones
ambientales como enfermedades, depredadores o competencia.
El problema con el modelo geométrico es que solo es
aplicable a aquellas especies que se reproducen estacionalmente. El modelo
geométrico puede describirse como un modelo de crecimiento de equilibrio
puntuado. La población se mantiene en un equilibrio relativo hasta la época de
apareamiento cuando nacen las crías y mueren aquellos viejos o sin experiencia,
aunque se puede notar una tendencia levemente exponencial, aunque la curva no
sea continua. Sin embargo, no todos los seres vivos son estacionales, las
generaciones pueden sobrelaparse y en tal caso se hace necesario un modelo que
represente tal modo de crecimiento poblacional.





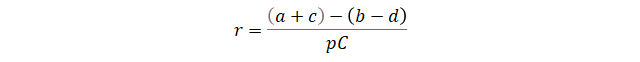



No hay comentarios:
Publicar un comentario