(Ciencias de Joseleg)(Biología) (Ecología) (La población) (Introducción) (Generalidades) (Historia) (Características) (Patrones de supervivencia y distribución de edades) (Crecimiento lineal y geométrico) (Crecimiento exponencial) (Crecimiento logístico) (Interacciones intraespecíficas) (Referencias bibliográficas)
Todos los seres vivos poseen la propiedad de superfecundidad, desde la ballena que se reproduce más lentamente hasta la bacteria que se duplica cada 20 minutos. Sin embargo, la superfecundidad no es compatible con un sistema real cuyos recursos son limitados. Es por esto que el modelo exponencial simple no puede decirnos que sucede una vez que los recursos se hacen limitados y como se desarrolla la catástrofe malthusiana. De hecho, la gran pregunta es ¿Qué tan catastrófica es esa catástrofe? Hay dos opciones, si los recursos no son renovables, pues la población decrece y se extingue, pero si los recursos si son renovables emerge un nuevo patrón, el modelo logístico con una curva sigmoide.
Figura 20. Modelo
logístico. El modelo exponencial es una aproximación al promedio de
lo que pasa cuando se alcanza la catástrofe mathusiana, asumiendo que los
recursos limitantes son renovables de manera continua.
Para lograr esta curva sigmoide, la tasa de cambio neta del
crecimiento poblacional debe poseer un término extra, que se asegure que a
medida que la población se acerca a un límite de recursos, el crecimiento
poblacional disminuya hasta que llegue a una tasa de cambio de cero (15).
Igual que en el exponencial la base es r x N,
pero el término entre paréntesis es una resta muy especial. En la resta se
encuentra un término llamado K. Cuando N se acerca a
K la división entre ambos se acerca a 1. Al acercarse a 1 la resta al
interior del paréntesis arroja un valor cercano a 0, lo cual paulatinamente
disminuye el producto r x N. Con este sencillo método matemático
es posible hacer más lenta la tasa de cambio de una forma que dependa del
tamaño de N. Ahora la pregunta es, ¿Qué significado biológico puede tener
K aparte de ser un mero artefacto matemático? Antes que nada expondremos
las dos fórmulas clásicas para la tasa de cambio (15),
y para calcular el tamaño en cualquier momento (52).
Despejamos los términos poblacionales a la izquierda y lo
demás a la derecha.
16
Separamos el denominador complejo empleando dos constantes
desconocidas invirtiendo el proceso de la suma de fraccionarios.
17
Ahora debemos saber por qué la constante
18
En la expresión anterior sabemos que todo el numerador es
igual a 1. En este punto debemos eliminar una de las constantes, vamos a elegir
aquella asociada al término más complicado.
19
Si queremos que este término se cancele asumiremos que N
= K solo para el numerador. Su eso es cierto, entonces se cumplirá
que.
20
Y, por lo tanto, sabremos el valor de la constante.
21
Ahora, determinaremos el valor de a.
22
Ahora que sabemos los valores de las constantes, seguimos.
23
Ahora integramos y despejamos el tamaño de la población.
24
Ahora determinaremos el valor de la población inicial para tiempo
igual a cero.
25
Con esto despejamos el valor de la quinta constante.
26
Con el valor de la quinta constante, reemplazamos en la
expresión para cualquier tiempo y simplificamos.
27
Von lo que obtenemos la ecuación final:
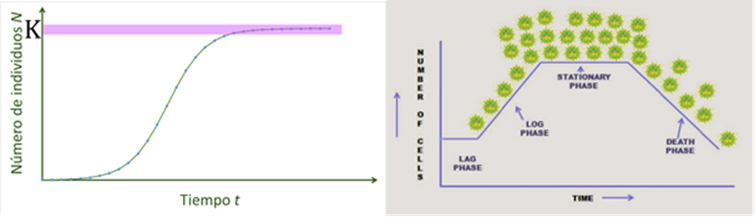
Figura 21. Capacidad
de carga. (Izquierda) El modelo logístico originado con la ecuación
(2) señalando la K o constante de capacidad de carga, en un sistema con
recursos renovables contínuos; ((Derecha) representación de un sistema logístico
real donde los recursos no son renovables.
La gráfica de la curva logística es semejante a la función
exponencial al inicio, generando una fase de adaptación y luego una fase
exponencial. Sin embargo, el término K provoca que a medida que la
población se aproxima a K su crecimiento se hace paulatinamente más
lento hasta llegar a un estado de equilibrio estático. Ahora debemos
preguntarnos por lo que sucede después de que se llega a la capacidad de carga K.
El mejor modelo ecológico para estudiar el crecimiento
logístico son las bacterias, y en este punto hay dos posibles curvas
dependiendo de si los recursos son renovables o no son renovables. Si los
recursos no son renovables la gráfica tiene forma de montaña, al igual que el
modelo teórico es exponencial hasta alcanzar el equilibrio, pero allí las
bacterias tienden a adaptarse y reducir sus necesidades, la competencia se hace
más fuerte en la medida que la tasa de muerte iguala a la tasa de nacimiento.
Finalmente, los recursos se agotan y la población decrece. En la anterior
simplificación del modelo logístico podemos apreciar un sistema con recursos no
renovables. El punto con los recursos no renovables es que convierten a
En un sistema de recursos renovales la población crece hasta que el consumo mantiene una población estable y pueden enlistarse dos subcasos. Si el flujo de recursos es continuo la curva de crecimiento es lisa como lo predice el modelo matemático. Si el flujo de recursos es cíclico la gráfica adquiere la forma de un sistema oscilante y dinámico que se mueve al interior de rangos máximos y mínimos, debido a que la capacidad de carga oscila entre un límite superior en la estación favorable como la primavera y un mínimo en la estación adversa como en el invierno.
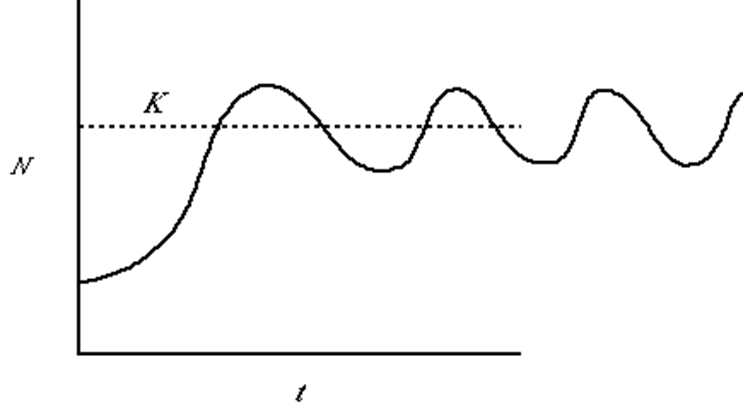
Figura 22. La
capacidad de carga como variable. En sistemas con renovación de
recursos cíclicos, la capacidad de carga será el eje de fluctuación de un
sistema en equilibrio dinámico.
Cuando se mide la variación de una población real, no
observamos los patrones pulsantes simétricos de la tabla anterior:
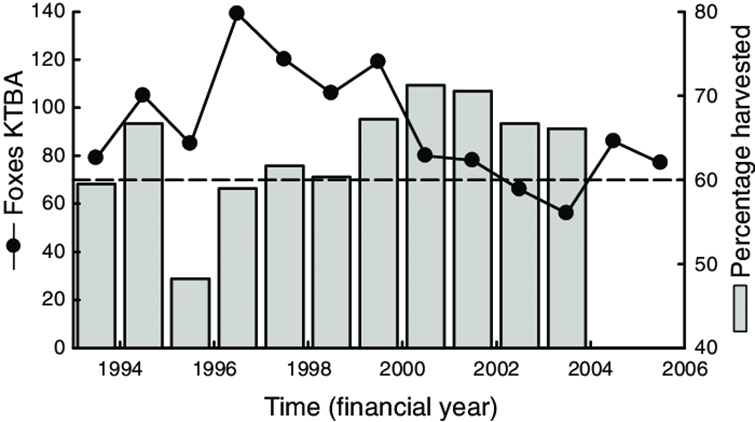
Figura 23. Número de zorros por unidad de tiempo, la
muestra se tomó en algún punto del equilibrio dinámico.
Es por esta razón, que aparte de aplicar un patrón cíclico, los modelos más precisos introducen una función aleatoria que provoca cambios no predecibles en las estaciones, un invierno moderado o más crudo, una primavera fría o más abundante etc:
Figura 24. Modelo de crecimiento logístico con una
capacidad de carga que cambia en base a variables cíclicas determinadas, y
variables azarosas no deterinadas.
Solo al introducir la función aleatoria, la gráfica en
equilibrio adquiere la estructura impredecible que vemos en las poblaciones
naturales.
El significado biológico de la constante K es el del
máximo valor de individuos que teóricamente pueden habitar un sistema en
ausencia de otras relaciones ecológicas como la depredación o la simbiosis. La
capacidad de carga K es el mayor aguante que tiene un ecosistema para
una población determinada, y en las gráficas se representa por el mayor punto
poblacional que alcanza la población.
Cuando los individuos se acercan a la capacidad de carga, los recursos se empiezan a hacer escasos aun cuando estos sean renovables, en consecuencia, menos descendientes son producidos y más muertes son provocadas por la hambruna, hasta alcanzar un nivel de pobreza general. Se refiere a pobreza general en el sentido en que todos los individuos apenas si subsisten con lo mínimo indispensable para mantener a la población estable. En este punto gran cantidad de descendientes mueren por cada generación.
Figura 25. Poniendo
a prueba el modelo. En la naturaleza, las especies se comportan como un
modelo logístico con recursos que se renuevan cíclicamente, y normalmente estos
ciclos son anuales.
Concentrémonos en lo que sucede cuando el sistema alcanza su
equilibrio:
- Todas las especies son superfecundas, lo que implica que
en condiciones ideales cada generación es más grande que la anterior;
- En el equilibrio las poblaciones no crecen;
- Gran parte de los descendientes en cada generación mueren.
A pesar de que Darwin analizó el modelo logístico simple estas tres condiciones
son igual de válidas, por lo que cabe la pregunta ¿Por qué sobreviven los pocos
que sobreviven?
Es evidente que una gran cantidad de individuos se están
muriendo, pero los sobrevivientes son el problema de la cuestión. Eso solo
puede resolver de tres formas:
- Que los que sobreviven, lo hacen totalmente al azar, su
supervivencia es un chiste cósmico un evento fortuito de la suerte;
- Los que sobreviven, lo hacen porque son de alguna manera
capaces de acaparar recursos en el sistema en equilibrio sin depender de la
suerte;
- Una mezcla de ambas respuestas, lo que genera un sistema
caótico y difícil de predecir. De aquí en adelante le daremos dos nombres a los
fenómenos, el primero, el del azar lo llamaremos DERIVA y al segundo el
de la capacidad superior le llamaremos SELECCIÓN.
Charles Darwin dependía de este fenómeno para poder dar
impulso a su propuesta teórica. Para el, el que algunos muy pocos individuos
sobrevivieran no tenía nada que ver con la suerte, por el contrario, se debía a
que los individuos eran superiores en sus relaciones ecológicas:
- Depredaban mejor y eran menos depredados;
- Tenían más mutualistas acompañantes que mejoraban sus
condiciones;
- Tenían menos parásitos por un sistema inmune superior a
sus pares;
- Obtienen más recursos inorgánicos (factores abióticos);
- Eran más tolerantes a los factores abióticos como la
temperatura, la baja disponibilidad de agua y minerales o una mayor tolerancia
a los venenos.
Con esto superaban a sus competidores intra e
interespecífcos cercanos. Esta es la naturaleza de la Selección Natural, la
cual a diferencia de muchas interpretaciones no es una fuerza vitalista, es una
deducción que emerge de
- las limitantes deducidas por los modelos de crecimiento
poblacional y
- por las interacciones ecológicas y de la comunidad
ecológica. Para Darwin, sin embargo, la interacción ecológica más importante de
la Selección Natural era la competencia intraespecífica y la razón es la
siguiente.
Debido a que, en cualquier modelo de crecimiento, los
individuos solo experimentan restricción de recursos en el equilibrio es válido
decir que la selección natural solo se hace evidente en ecosistemas en
equilibrio, donde las interacciones de la población, la comunidad y el
ecosistema se hacen estables. Bajo tales condiciones un individuo debe afrontar
competencia contra otros individuos de su misma especie, a esto se lo denomina
competencia intraespecífica. Esto se debe a que los individuos de una misma
especie tienen todos los mismos requerimientos, sus nichos son los mismos y por
lo tanto compiten de forma directa por ellos. La lucha puede ser directa
Por ejemplo, de competencia intraespecífica es la lucha por
parejas para la reproducción sexual, donde machos y/o hembras pelean entre sí
para acceder a la posibilidad de la reproducción. Darwin denominó esto
selección sexual. La lucha también puede ser indirecta acaparando egoístamente
recursos relacionados con las interacciones de la comunidad como la depredación
(relación depredador – presa) o la simbiosis (comensalismo, parasitismo,
mutualismo, sinecrosis). En últimas, la selección natural es un subproducto de
todas las interacciones individuo con su ecosistema, es decir la suma de los
factores bióticos y abióticos. Alterar una sola variable puede afectar los
patrones de selección natural en todo el sistema, disminuyéndola para algunos e
incrementándola para otros. Si la selección natural es muy fuerte la población
será condicionada inevitablemente a la extinción.
Finalmente, el modelo logístico nos permite dar el nombre a
dos estrategias de vida. La estrategia de vida es el modo en que el tamaño de
la población crece para sacar ventaja de algunas interacciones con el
medioambiente. En base a esto señalaremos dos. La estrategia de vida r se
relaciona con especies con altas tasas de crecimiento, nacen muchos, tienen
ciclos de vida corto y requiere pocos recursos para subsistir. Estas especies
favorecen la cantidad sobre la calidad, las crías son reemplazables y en cada
ciclo se genera una gran mortandad. La estrategia de vida

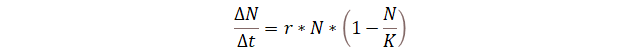
















No hay comentarios:
Publicar un comentario