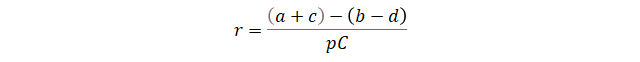Modelo de crecimiento poblacional exponencial

(Ciencias de Joseleg)(Biología) (Ecología) (La población) (Introducción) (Generalidades) (Historia) (Características) (Patrones de supervivencia y distribución de edades) (Crecimiento lineal y geométrico) (Crecimiento exponencial) (Crecimiento logístico) (Interacciones intraespecíficas) (Referencias bibliográficas)

  Intuitivamente sabemos que una población con generaciones sobrelapantes tendrá un crecimiento más continuo, una curva suave, pero al mismo tiempo deberá ser exponencial, es decir, la curva deberá tener una forma de j continua:

Figura 16.  Crecimiento exponencial. El modelo exponencial simple modela a una población que no presenta mayores dificultades por factores ambientales como los depredadores, las enfermedades o los competidores.

Para lograr una descripción de esa manera emplearemos una nueva definición para la tasa de cambio de la población con respecto al tiempo (8). Para este modelo asumiremos de  es una constante, pero la tasa reproductiva no es constante como tal, la tasa reproductiva depende de  veces el tamaño de la población, por lo que poblaciones más grandes crecerán a mayor velocidad. Existe un punto de viraje en la población que matemáticamente se conoce como punto de inflexión, ecológicamente este puto de no retorno se manifiesta como el aumento desmesurado de una especie en un ecosistema, es decir, una plaga. El resultado es la fórmula (14). En este caso r no es la pendiente ya que ese concepto no aplica para una curva exponencial. De hecho, un detalle importante de las curvas exponenciales es que poco a poco su velocidad de crecimiento sobrepasa la de una recta.

8

Deducción

Partiendo de (8) que representa la tasa de cambio de la población, deberemos obtener la ecuación del modelo exponencial mediante un procedimiento de cálculo llamado integración de ecuaciones diferenciales. El primer paso es tejar todos los términos de población a la izquierda, y todo lo demás a la derecha. Integramos ambos lados de la expresión.

9

A la izquierda se integra con respecto al tamaño de la población y a la derecha con respecto al tiempo. A la derecha, la constante r sale de la integral.

10

11

Finalizada la integración, debemos despejar la variable N para que quede en términos del tiempo, fíjese que los demás términos son constantes.

12

13

Solo falta determinar cuál es el valor de la constante de proporcionalidad, o al menos sus unidades. Normalmente la constante y el tiempo se reemplazan sin unidades, por lo que las unidades del número de individuos son portadas por la constante de proporcionalidad, así que esta debe ser un tamaño de población constante. El único valor constante es el tamaño inicial.

14

Propiedades biológicas del modelo de crecimiento exponencial

Cuando se compara el crecimiento exponencial con el crecimiento lineal una propiedad salta a la vista, aun cuando al inicio ambos pueden parecer muy semejantes, poco a poco el crecimiento exponencial acelera de forma tal que excede con gran facilidad al crecimiento lineal. Esto implica que los seres vivos que adoptan el crecimiento exponencial tienen una fase de crecimiento lenta que representa una adaptación al medio y luego sus números cercen de forma abrupta. La pregunta es, ¿es posible que todos los seres vivos sean capaces de sustentar una tasa de crecimiento exponencial? Y ¿es posible que un ser vivo bajo crecimiento exponencial sea capaz de crecer de forma indefinida? Si los seres vivos no son entidades aisladas, sino que por el contrario interactúan con el medioambiente ¿Cómo afectaran al medioambiente si empiezan a incrementar su población sin control?

Algunos de los supuestos del modelo de crecimiento exponencial, como una tasa de crecimiento per cápita constante “r” o una tasa de crecimiento neta que tiende a infinito, pueden parecer un poco realistas, por lo que es razonable preguntarse si las poblaciones en la naturaleza realmente se acoplan al modelo exponencial. La respuesta sigue siendo si, las poblaciones naturales pueden crecer a tasas exponenciales durante períodos de tiempo relativamente cortos en presencia de recursos abundantes, baja densidad de depredadores, competidores y parásitos.

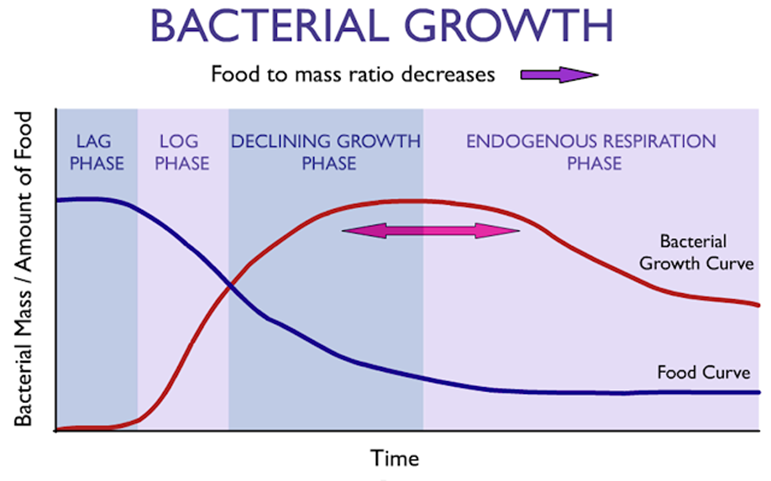
Figura 17.  Crecimiento bacteriano. Gráfica de una población bacteriana típica basada en múltiples muestreos experimentales, "datos con los que no contaba Malthus, pero que sin duda señalan su punto". El crecimiento exponencial no puede mantenerse indefinidamente en un sistema cuyos recursos son limitados.

Sin embargo, hay que recordar que el modelo original malthusiano contiene el concepto de la “catástrofe por los recursos limitados” así que el punto límite de crecimiento también hace parte fundamental de los supuestos del modelo exponencial simple, después de todo, solo un economista creería que es posible sustentar un crecimiento infinito sobre recursos finitos.

Las bacterias como una población malthusiana

La producción de cerveza o cualquier bebida fermentada nos muestra como en un sistema real, el crecimiento exponencial no es sustentable a largo plazo, pero a corto plazo si se manifiesta. En un biorreactor para la producción de alcohol fermentado se tiene una fuente de energía que llamaremos simplemente azúcar, algunos biocompuestos nutritivos y mucha agua. El proceso inicia con la adición de una pequeña población de bacterias. Con el tiempo las bacterias inician su crecimiento siguiendo el patrón del modelo exponencial. Durante esta fase se produce alcohol que es básicamente un desecho, es decir un producto que contamina el agua para las bacterias, y al mismo tiempo consumen el azúcar que no es renovado. Cuando las toxinas se acumulan “es decir el alcohol” y los alimentos se acaban el crecimiento exponencial se limita y la curva toma una forma rectilínea horizontal por un tiempo, allí las bacterias empiezan a consumir con menos velocidad, pero su destino es inevitable ya que si no comen se mueren. Finalmente, la hambruna y la contaminación “por alcohol” genera una muerte masiva y una disminución de la población de bacterias y en este punto nuestra bebida alcohólica ha sido fermentada.

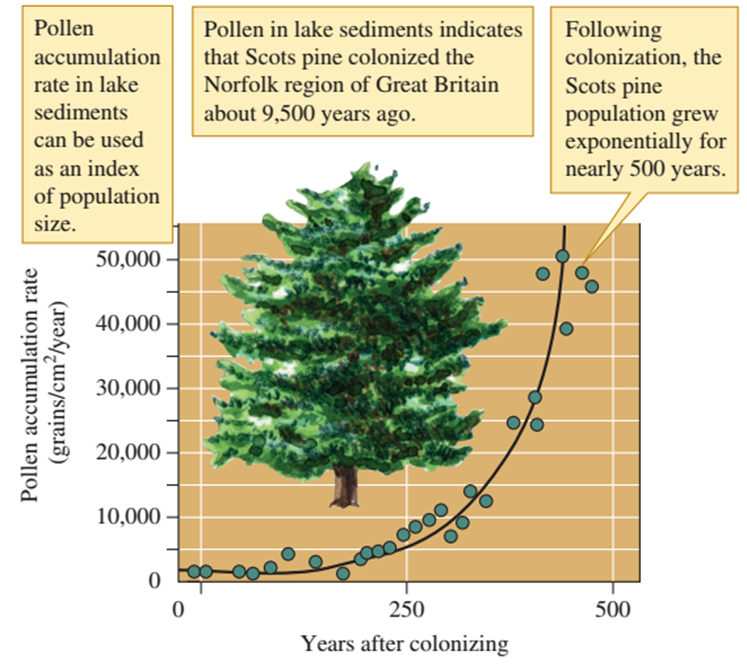
Figura 18.   Crecimiento exponencial de una población colonizadora de pinos escoceses. Empleando (1) la acumulación de polen en los sedimentos de lagos por unidad de área por año. (2) Estos sedimentos indican que los pinos escoceses invadieron Gran Bretaña hace unos 9500 años, (3) después de los cuales, el crecimiento fue marcadamente exponencial por 500 años.

A medida que la última era de hielo terminaba, las poblaciones de árboles en el Hemisferio Norte seguían a los glaciares en retroceso hacia el norte. Los ecologistas han documentado estos movimientos estudiando los sedimentos de los lagos, donde el polen de las especies de árboles polinizados por el viento es o fue especialmente abundante. La aparición del polen de una especie de árbol en un sedimento de lago es un registro de su establecimiento cerca del lago. La fecha de cada establecimiento se puede determinar utilizando la concentración carbono-14 para determinar la edad de la materia orgánica a lo largo de un perfil de sedimento.

Los registros de polen también se han utilizado para estimar el crecimiento de varias poblaciones de árboles postglaciales en Gran Bretaña. Bennett (1983) estimó el tamaño de la población y el crecimiento contando el número de granos de polen de cada especie de árbol depositada en los sedimentos de los lagos. Al contar el número de granos de polen por centímetro cuadrado que se depositan cada año, Bennett fue capaz de reconstruir los cambios en las densidades de la población de árboles en el paisaje circundante. Su estudio reveló una interesante imagen del crecimiento de las poblaciones de árboles postglaciales en las Islas Británicas.

Las poblaciones de las especies de árboles estudiadas crecieron a tasas exponenciales de 400 a 500 años después de su aparición inicial en el registro de polen. La Figura 18 muestra el aumento exponencial de la abundancia de pino silvestre, Pinus sylvestris, que apareció por primera vez en el registro polínico de los lagos estudiados hace unos 9.500 años.

Condiciones para el crecimiento exponencial

Las poblaciones naturales de organismos tan diferentes como las diatomeas, las ballenas, bacterias y árboles pueden crecer a tasas exponenciales. Sin embargo, por diferentes que sean estos organismos, las circunstancias en que sus poblaciones crecen a tasas exponenciales tienen mucho en común. Todos comienzan su crecimiento exponencial en entornos favorables a bajas densidades de población. Los árboles estudiados por Bennett comenzaron a bajas densidades debido a que estaban invadiendo un nuevo territorio previamente desocupado por la especie. Las floraciones de primavera de diatomeas planctónicas son el resultado del crecimiento exponencial de la población en respuesta a los aumentos estacionales en nutrientes y luz.

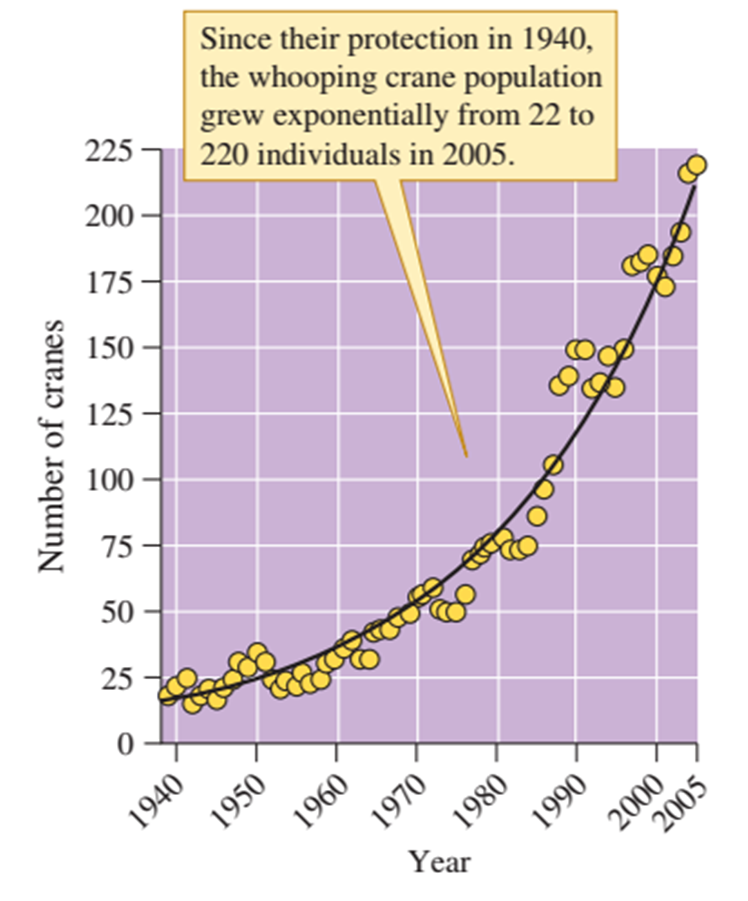
Figura 19.  Salvando de la extinción. La caza excesiva y la destrucción del hábitat de la grulla trompetera redujeron su especie a una sola población, pero la protección y manejo ha permitido una rápida restauración de sus números.

La grulla trompetera “Grus americana” proporciona otro ejemplo de crecimiento exponencial tras la protección y el manejo cuidadoso. La caza y la destrucción del hábitat redujeron la población de grullas a 22 individuos en 1940. En ese momento, se sabía que esta población remanente de grullas invadió en la costa del Golfo de Texas, pero sus áreas de reproducción septentrional eran desconocidas. Más tarde se descubrió que se reproducían en el Parque Nacional Wood Buffalo en Canadá. Bajo la protección total y el manejo cuidadoso tanto en Canadá como en los Estados Unidos, la población de grullas migratorias ha crecido exponencialmente de 22 en 1940 a 220 individuos en 2005.

Estos ejemplos sugieren que el crecimiento exponencial de la población puede ser muy importante para las poblaciones durante el proceso de establecimiento en nuevos ambientes, durante la explotación de condiciones transitorias, favorables y durante el proceso de recuperación de alguna forma de presión selectiva o deriva genética. Sin embargo, como como vemos en el equilibrio natural real, y como predice Malthus, llega el momento de la catástrofe. En la naturaleza, el crecimiento demográfico debe eventualmente disminuir y el nivel de población regularse por medio de interacciones ecológicas que denominamos en su conjunto como la Selección Natural. 

 

Modelo matemático de crecimiento poblacional, lineal y geométrico

(Ciencias de Joseleg)(Biología) (Ecología) (La población) (Introducción) (Generalidades) (Historia) (Características) (Patrones de supervivencia y distribución de edades) (Crecimiento lineal y geométrico) (Crecimiento exponencial) (Crecimiento logístico) (Interacciones intraespecíficas) (Referencias bibliográficas)

  Antes de introducir el problema del crecimiento exponencial, se trabajará con el modelo matemático lineal para introducir una serie de nombres de variables que serán empleados en todos los modelos de dinámica de poblaciones. Entre ellos cabe destacar a los símbolos para el tamaño de la población, la designación del tiempo y el mucho más importante, tasa de crecimiento de la población. Aunque la tasa de crecimiento de la población y el tiempo poseen significados diferentes dependiendo del modelo a trabajar, sus significados intrínsecos son semejantes y serán trabajados con más profundidad en los siguientes artículos. El objetivo primordial no es las fórmulas matemáticas, por el contrario, es el análisis gráfico.

Figura 13.  Modelo lineal. La variable dependiente es el número total de individuos que será simbolizado con la letra (N) mayúscula, emplearemos (n) minúscula en caso de que estemos analizando una fracción de la población total, como por ejemplo el número de machos, el número de crías o el número de hembras. La suma de todos los (n) debe dar como resultado el número total de la población (N). Por lo tanto, es posible expresar el problema en términos de un plano cartesiano.

Modelo lineal

Ya sé que las poblaciones no crecen linealmente, pero el modelo inicial siempre es la base de todos estos tipos de cálculos.

Una población en el plano cartesiano

Dado que los modelos de crecimiento exponencial son básicamente copias de conceptos de dinámica, se aconseja repasar lo trabajado en el movimiento uniformemente acelerado. Sin embargo, si usted se encuentra en educación básica introduciremos brevemente algunos conceptos y simbología mediante la gráfica de la línea recta. Los modelos de crecimiento exponencial son sistemas de dos variables, una independiente y la otra dependiente. La variable independiente es el tiempo, la cual solo tiene un eje posible y es el positivo, debido a que el tiempo siempre avanza hacia adelante. Esta variable será simbolizada con la letra (t).

Definiendo la tasa de crecimiento poblacional en el modelo lineal

En base a la gráfica en el plano cartesiano podemos emplear la ecuación de la recta para poder definir un concepto extra que es muy importante en la dinámica de poblaciones y es la tasa de crecimiento de la población. En una línea recta la tasa de crecimiento poblacional es homóloga a la pendiente de la recta. Es decir si tenemos la ecuación de la recta podemos reemplazarla con las variables de nuestra recta, las “Y” se reemplazan por el tamaño de la población y las “X” por el tiempo, lo cual nos deja la ecuación expresada del siguiente modo:

  2

  3

Tamaño poblacional en función de la tasa de crecimiento intrínseca, el tiempo y el tamaño inicial como un modelo de línea recta.

“N(t)” representa el tamaño de la población en cualquier momento t. La variable “t” representa el tiempo que puede ser expresado en segundos, minutos, días años o más. “N(t)” representa el tamaño de la población al inicio de la medida y en ocasiones puede ser representada como “N(0)” que se lee como el tamaño de la población en el tiempo cero. Mientras que “m” es la pendiente de la recta y representa la tasa de crecimiento de la recta. Sin embargo, lo que crece no es una recta abstracta, sino una población, por lo que generalmente se cambia “ ” por la tasa reproductiva neta de la población o “r”.

  4

  5

Crecimiento neto de la población en un modelo lineal.

La fórmula para encontrar la pendiente de una recta cualquiera (4) nos sirve análogamente para encontrar la tasa de crecimiento en un modelo lineal (5). Cabe destacar que las diferencias pueden ser reemplazadas por el símbolo delta (Δ) que simboliza la diferencia de un punto final y un punto inicial (5). El delta representa una resta entre dos valores muy diferentes. Pero a medida que los valores para la resta se hacen más y más cercanos, (Δ) se reemplaza por (ẟ) que implica la existencia de una resta entre valores infinitamente cercanos entre sí (5). El modelo de crecimiento lineal nos otorga dos datos o fórmulas comunes a los demás modelos de crecimiento más empleados, el exponencial y el logístico. El primero es la tasa de cambio (5) que se define como el cambio de la población con respecto al cambio de tiempo a un nivel infinitesimal, y la otra es la fórmula para calcular el tamaño de la población para cualquier momento t (3). Sin embargo, otros modelos nos exigirán un mayor nivel matemático.

Diferentes formas de ver la constante r

La matematización de las poblaciones debe poder representar al organismo sin importar la especie de la que se está hablando como girasoles, elefantes o seres humanos. Las gráficas que se manejan siempre serán de número de individuos en el eje (Y) contra el tiempo en el eje (X). Cuando se realiza la gráfica en un sistema lineal aparece una variable denominada tasa de crecimiento de la población (r). La tasa de crecimiento a escala global está regulada por dos variables, los nacimientos por cada individuo y las muertes por cada individuo. La relación se modelaría en base a la siguiente fórmula simple.

6

Componentes de la tasa de crecimiento intrínseca o percápita de la población.

Donde (a) representa la tasa de nacimientos y (b) la tasa de muertes. El problema es que, en la realidad la fórmula es expresada en términos un valor arbitrario de individuos, esto se hace dividiendo a y b en una constante de individuos llamados “per cápita”. A esa constante la llamaremos pC. En adición a las tasas de muerte y nacimiento existe otra variable que debe tenerse en cuenta a la hora de analizar la dinámica de poblaciones y es la dispersión. La dispersión se define como los movimientos de individuos con respecto a las fronteras del territorio. Si los individuos salen de la frontera la población disminuye, pero si ingresan a las fronteras la población aumenta. La salida de individuos se denomina emigración y el ingreso se llama inmigración. Estas dos variables también afectan a la constante r. Donde (c) son los individuos inmigrantes y (d) los emigrantes.

Figura 14.  Nacimientos y muertes. Gráficas de crecimiento exponencial "naranja", tasa de nacimiento "azul claro = a" y tasa de muerte "azul oscuro = b". La población no cambia su tamaño cuando a = b, pero cuando hay una diferencia entre ambos valores la población cambia. si a > b la población crece; si a < b la población decrece.

La tasa de crecimiento intrínseca se define como la expresión de “r” máxima, es decir cuando la población se encuentra en condiciones ideales para su crecimiento. Estas condiciones son la suma de los ideales de las interacciones ecológicas. Por ejemplo, las relaciones perjudiciales como depredación, parasitismo y competencia “interespecífica e intraespecífica” son de 0. Y las relaciones positivas como fuentes de alimentos y recursos abióticos son óptimas. En tal caso, la población crecerá a su máximo siguiendo un patrón exponencial mientras que las relaciones ecológicas estén a su máximo. Las consecuencias del crecimiento exponencial ya han sido discutidas de forma extensa mediante la interpretación malthusiana.

Modelo geométrico

7

El modelo geométrico se obtuvo por métodos más empíricos, consta de las variables de tamaño poblacional del modelo anterior, pero cambia la constante r por la constante λ que representa la cantidad de crías promedio de una determinada población elevado al tiempo (7).

Figura 15.  Crecimiento geométrico. El modelo geométrico modelaría una población que crece estacionalmente, pero que no está sometida a presiones ambientales como enfermedades, depredadores o competencia.

El problema con el modelo geométrico es que solo es aplicable a aquellas especies que se reproducen estacionalmente. El modelo geométrico puede describirse como un modelo de crecimiento de equilibrio puntuado. La población se mantiene en un equilibrio relativo hasta la época de apareamiento cuando nacen las crías y mueren aquellos viejos o sin experiencia, aunque se puede notar una tendencia levemente exponencial, aunque la curva no sea continua. Sin embargo, no todos los seres vivos son estacionales, las generaciones pueden sobrelaparse y en tal caso se hace necesario un modelo que represente tal modo de crecimiento poblacional.